How to reflect across y=xThere is no simple formula for a reflection over a point like this, but we can follow the 3 steps below to solve this type of question First , plot the point of reflection , as shown below Second , similar to finding the slope, count the number of units up and over from the preimage to the point of reflection Given a point (x1, y1) and an equation for a line (yStep 1 First we have to write the vertices of the given triangle ABC in matrix form as given below Step 2 Since the triangle ABC is reflected about xaxis, to get the reflected image, we have to multiply the above matrix by the matrix given below Step 311/2/21 If the vector is v ∈ R 3, then the matrix that reflects about the plane is R v = I − 2 v v T It is easy to check that R v flips the sign of any vector which is a multiple of v and acts as identity on any vector perpendicular to v See Householder transformation for more details In particular, the plane y = z is perpendicular to ( 0, 1 2

Linear Transformation Combination Of Ccw 90 Rotation And Reflection On Y X With Product Of Matrix Youtube
Reflection in y=x matrix
Reflection in y=x matrix-Play this game to review Geometry B(2, 4) Reflect over the line y = xNov 04, 15 Write a rule in function notation to describe the transformation that is a reflection across the yaxis A Rx0(X,Y) B Ry0(X,Y) C Ryx(X,Y) D Rx1(X,Y) math Triangle ABC below is reflected across the yaxis and then translated 1 unit right and 2 units downThe incident ray, the reflected ray, and the normal to theLinear transformations with Matrices lesson 10 Reflection in the line y=x In this lesson we talked about how to reflect a point in the line y=x



Modeling Transformation Ppt Download
CT (x) = T (cx) Where T is your transformation (in this case, the scaling matrix), x and y are two abstract column vectors, and c is a constant If these two rules work, then you have a linear transformation ) Comment on eamanshire's post "Usually you should justReflect Again The point is the image of the point after reflection in the line To find use the fact that the midpoint of is on the line and the line segment is perpendicular to the line and show that where Hence establish another proof that the matrix gives a reflection in the lineThis lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitter
Geometry reflection A reflection is a "flip" of an object over a line Let's look at two very common reflections a horizontal reflection and a vertical reflectionThe matrix representation for a reflection in the line y = mxThe handout, Reflection over Any Oblique Line, shows how linear transformation rules for reflections over lines can be expressed in terms of matrix multiplication After showing students matrix multiplication based transformation rules, they better understand why matrix multiplication is done the way it is
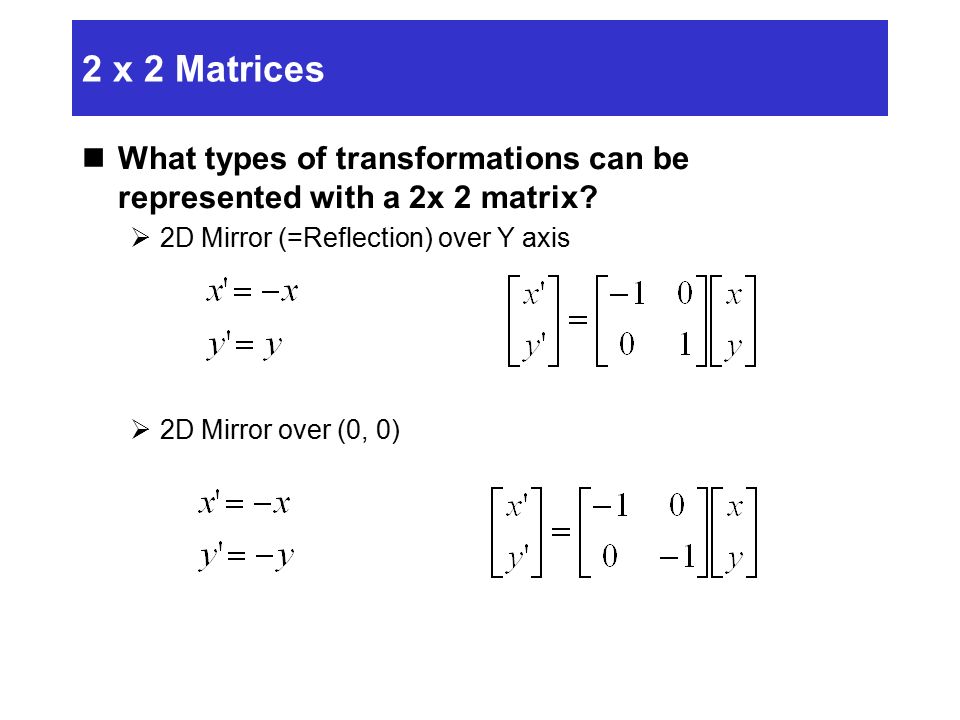
Reflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxisDerive the matrix in 2D for Reflection of an object about a line y=mxc written 25 years ago by profvaibhavbadbe ♦ 780 modified 14 months ago by sanketshingote ♦ 570 2d transformation matrixReflection In The Line Y X Matrix images, similar and related articles aggregated throughout the Internet




Matrix Representation Of 2d Transformation Javatpoint




Matrix Reflections Youtube
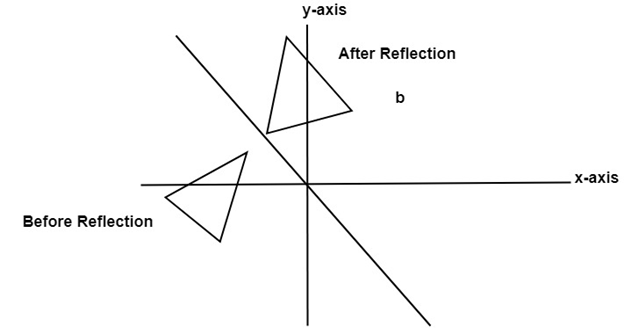
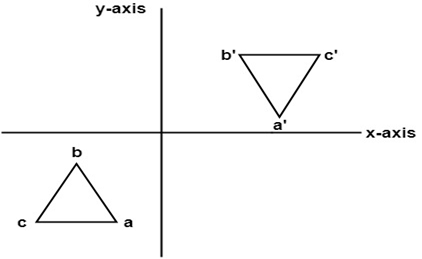
Reflections are isometries As you can see in diagram 1 below, $$ \triangle ABC $$ is reflected over the yaxis to its image $$ \triangle A'B'C' $$ And the distance between each of the points on the preimage is maintained in its image7/7/ How do you prove that the point P (x,y) becomes P' (y,x) after reflecting upon the line y=x?The linear transformation matrix for a reflection across the line y = mx is 1 1 m2(1 − m2 2m 2m m2 − 1) My professor gave us the formula above with no explanation why it works I am completely new to linear algebra so I have absolutely no idea how to go about deriving the formula



Two Dimensionaltransformations



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube
17/4/21 Reflection over the xaxis is a type of linear transformation that flips a shape or graph over the xaxis Every point above the xaxis is reflected to its corresponding position below the xaxis;Supposing we wish to find the matrix that represents the reflection of any point (x, y) in the xaxisThe transformation involved here is one in which the coordinates of point (x, y) will be transformed from (x, y) to (x, y)For this to happen, x does not change, but y must be negatedWe can therefore achieve the required transformation by multiplying y by minus one (1)This video shows reflection over y = x, y = − x A reflection that results in an overlapping shape Show Video Lesson This video shows reflection over the xaxis, yaxis, x = − We use coordinate rules as well as matrix multiplication to reflect a polygon (or polygon matrix) about the xaxis, yaxis, the line y = x or the line y = x




Match Each Linear Transformation With Its Matrix A Chegg Com



Reflection In 2 D
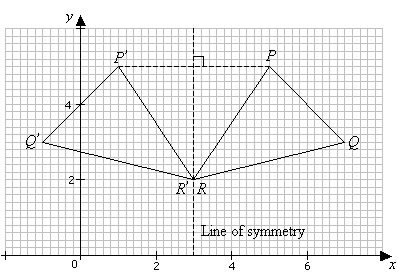
1 If the line of reflection is the xaxis, then m = 0, b = 0, and (p, q) → (p, q) 2 If the line of reflection is y = x, then m = 1, b = 0, and (p, q) → (2q/2, 2p/2 = (q, p) 3 If the line of reflection is y = 2x 4, then m = 2, b = 4, (1 – m2)/(1 m2) = 3/5, (m2 – 1)/(m2 1) = 3/5,3/5/21 Example Of Reflection Over Y=X / Reflection MathBitsNotebook(Geo CCSS Math) • this video shows reflection over y = x, y = − xIn fact, if i →, j → is the canonical (orthonormal) basis, the first column is the image of i →, thus has a polar angle equal to 2 α the second column, which is the image is j →, is orthogonal to the first one, with norm one Thus it is necessarily ( sin ( 2 α) − cos
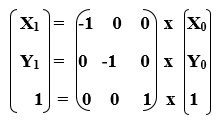



2d Reflection In Computer Graphics Tutorial And Example




Reflection Transformation
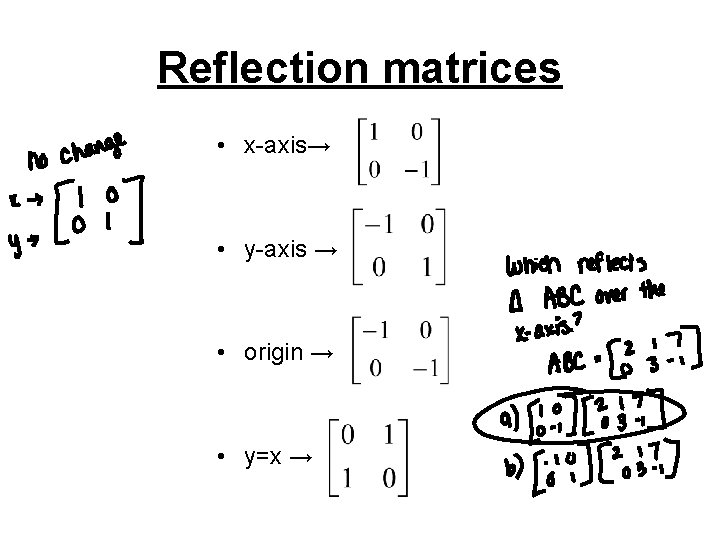
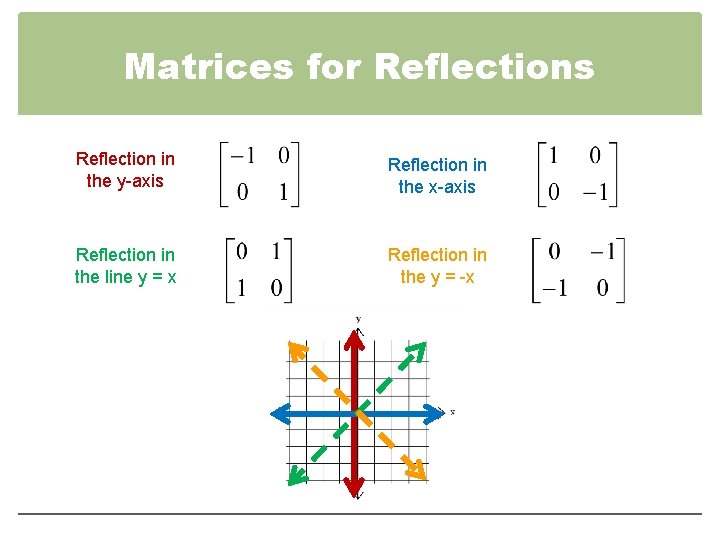
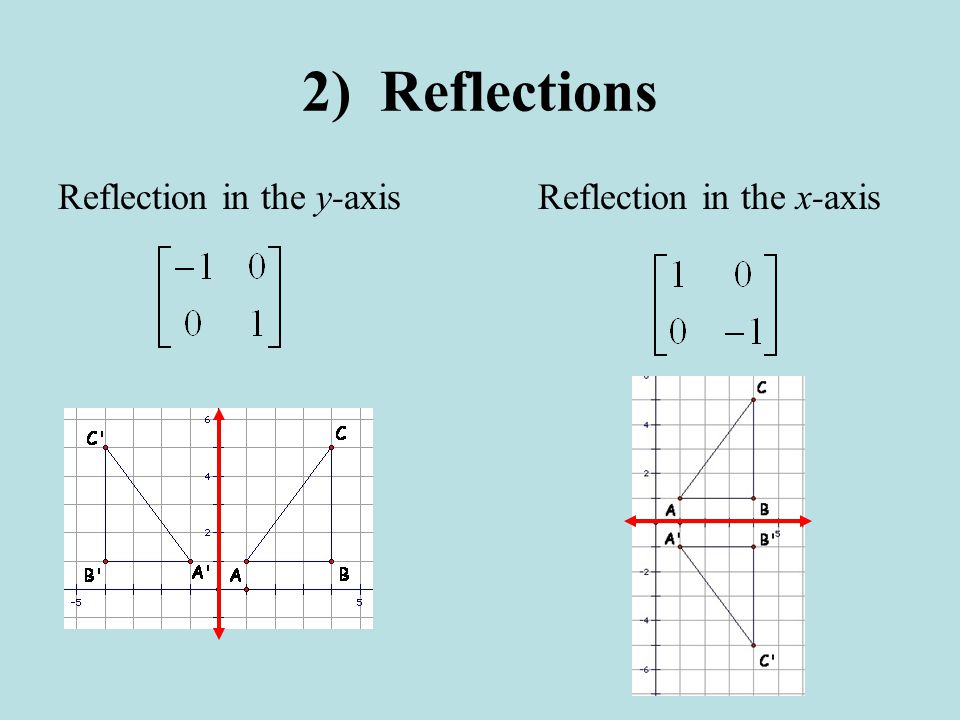
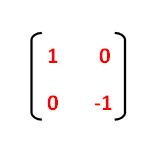
Reflection line points ShareY x y ' ' 1 # $ % % % & ' (((" 1 m y y x x " " ' ') x x * , ' 2 y y ' 2 4 Rotate the plane about the origin thr ough an angle of !When we want to create a reflection image we multiply the vertex matrix of our figure with what is called a reflection matrix The most common reflection matrices are for a reflection in the xaxis $$\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$$ for a reflection in the yaxis $$\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$$ for a reflection in the origin $$\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$$ for a reflection in the line y=x



Matrices In Computer Graphics Dalao S World



Computer Graphics Reflection Javatpoint
25/5/21 Y X W I 3) reflection across the yaxis x y B S Z 4) reflection across the xaxis x y T R I 5) reflection across the yaxis x y M P Z ©j p2D0j1L5t lKVuJtqaD zSeo^fNtuwpalrYei ELdLfCCd n vAOlklA AroiKgLhwtHsj YrqeBsJelrmvPefR Y KMzaHd_eC wwviFtZhF dIJnmfHiAnfiGtJeX nGpeSo_mAeItXrHyxFeb 02, 13 Reflection Over y = 2 With Rule by Lance Powell on Feb 02, 137/4/15 "Reflecting about the line y= x" the vector is mapped into < 0, 1> and the vector is mapped into So we must have tex\begin{bmatrix}a & b \\ c & d \end{bmatrix}\begin{bmatrix}1 \\ 0 \end{bmatrix}= \begin{bmatrix} 0 \\ 1\end{bmatrix}/tex and tex\begin{bmatrix}a & b \\ c & d \end{bmatrix}\begin{bmatrix}0 \\ 1 \end{bmatrix}=21/1/ When reflecting over the line y=x, we switch our x and y, and make both negative Reflection Over Y = X In order to define or describe a reflection, you need the equation of the line of reflection



2



1
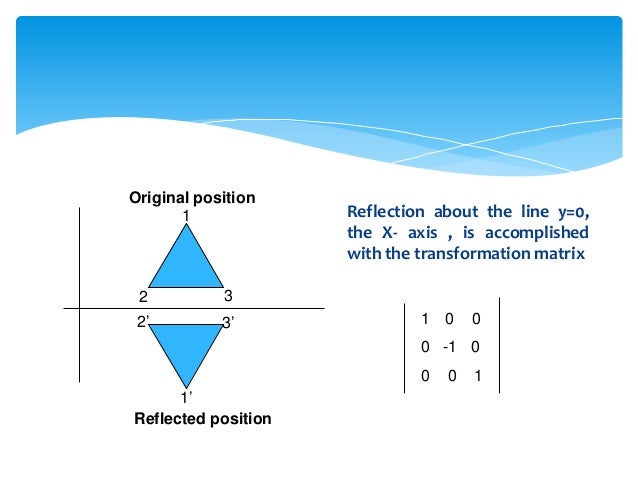
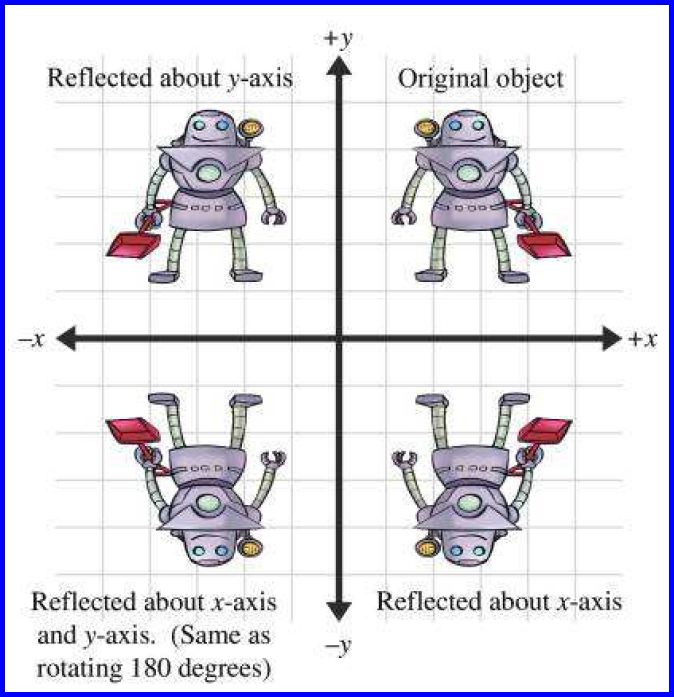
Reflection Transformations in 2Space Let such that and suppose that we want to reflect across the axis as illustrated Thus the coordinate of our vector will be the opposite to that of our image The following equations summarize our image Thus our standard matrix is , and in form we get that Of course there are other types of reflectionFor example, when reflecting the point (2,5) over y=x it becomes (5,2) This is very simple, but why does it work?Y (x, y) → (–x, y) or r y(x, y) = (–x, y) Both are read "the refl ection over the yaxis maps point (x, y) onto point (–x, y)" Mental Math Use matrices A, B, and C below Tell whether it is possible to calculate each of the following A = 23 –1 7 B = 4 05 C = 63 0 –12 a A B b AB c BA d BC A 63 y x 0 B = x(, ) A == x, (y) Lesson 46 Matrices for Refl ections




1 Point Match Each Linear Transformation With Its Chegg Com



Math Alive Geometry 1
/5/21 How to do a reflection of y=xReflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45°Ordered pair rules reflect over the xaxis (x, y), yaxis (x, y), line y = x (y, x) The following diagram shows how to reflect points and figures on the coordinate plane Examples shown areコレクション reflection over the line y=x calculator How to do a reflection over the line y=x Feb 02, 13 Educreations is a community where anyone can teach what they know and learn what they don't Our software turns any iPad or web browser into a recordable,8/1/ Reflection along Xaxis In this kind of Reflection, the value of X is positive, and the value of Y is negative We can represent the Reflection along xaxis by following equation



Matrices As Transformations
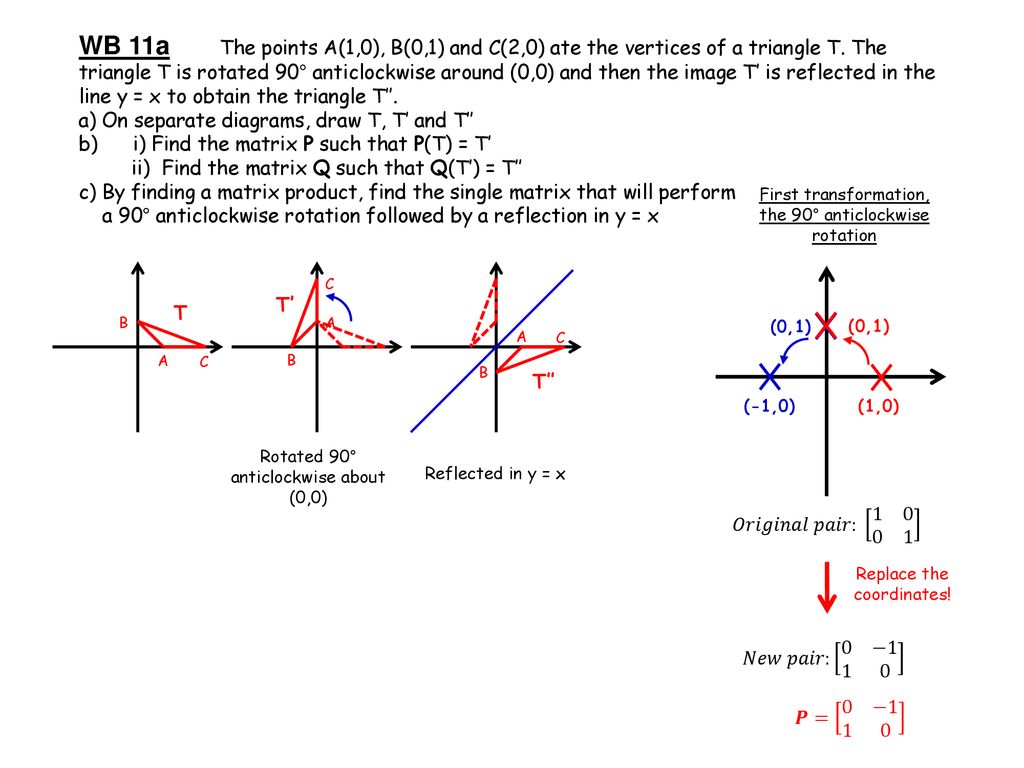



Fp1 Matrices Transformations Ppt Download
Point reflection, also called as an inversion in a point is defined as an isometry of Euclidean space It can also be defined as the inversion through a point or the central inversion Use our online point reflection calculator to know the point reflection for the given coordinates5 Translate by (0, b) Expr essing this in matrix form and using Mathematica yields Figure 5 Apply the double angle formulas to the output and you get the same r esult we got earlier I suspect that theWcorr = modwtcorr(w1,w2) returns the wavelet correlation by scale for the maximal overlap discrete wavelet transforms (MODWTs) specified in w1 and w2 wcorr is an Mby1 vector of correlation coefficients, where M is the number of levels with nonboundary wavelet coefficients If the final level has enough nonboundary coefficients, modwtcorr returns the scaling correlation in the final
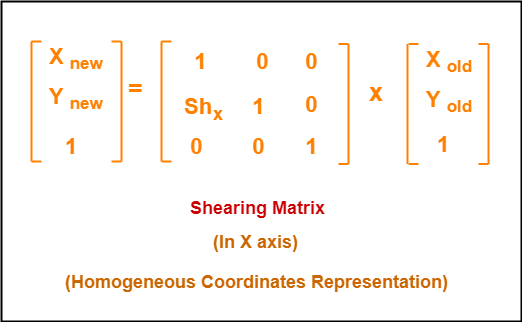



2d Shearing In Computer Graphics Definition Examples Gate Vidyalay




Reflection Rules How To W 25 Step By Step Examples
X,y>x,y (reflection over y axis) – GeoGebra Transformations 8th Grade Math – GeoGebra Reflections Through the Axes and the lines y=x and y=x Identifying Properties of Reflections Which statements are Geometry Reflection (examples, solutions, videosSolutions to More Matrix Transformations Transformation Matrix Transformation Matrix A Reflection in the x axis 10 01 ⎛⎞ ⎜⎟⎝⎠− N Rotation by 45°clockwise about the origin 11 22 11 22 ⎛⎞ ⎜⎟ ⎜⎟ ⎜⎟ ⎜⎟− ⎝⎠ B Rotation by 30°clockwise about the origin 31 22 13 22 ⎛⎞ ⎜⎟ ⎜⎟ ⎜⎟ ⎜⎟− ⎝⎠ OY X Graph Reflection Algebraic Representations of Reflections reflections worksheet properties axis graph triangle algebraic reflection line onlinemath4all its along paper representations vertices pqr homeschooldressage label Reflection over y=x Reflections across y=x – GeoGebra What is the equation for the line of reflection?
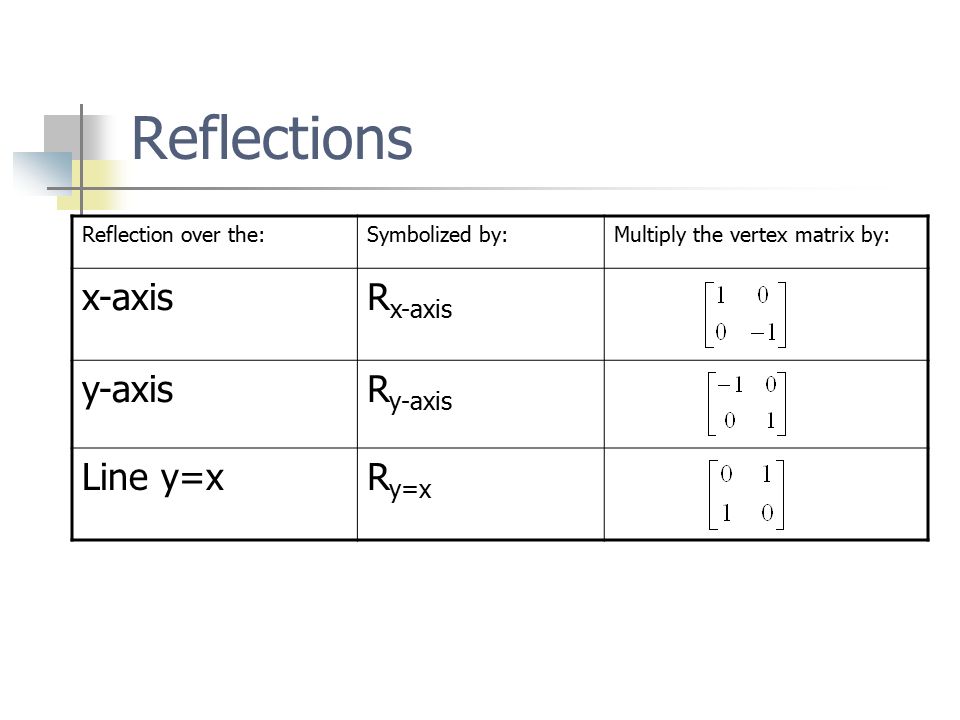



2 4 Modeling Motion With Matrices Pre Calc A Vocabulary Transformations Translation Reflection Rotations Dilations Ppt Download
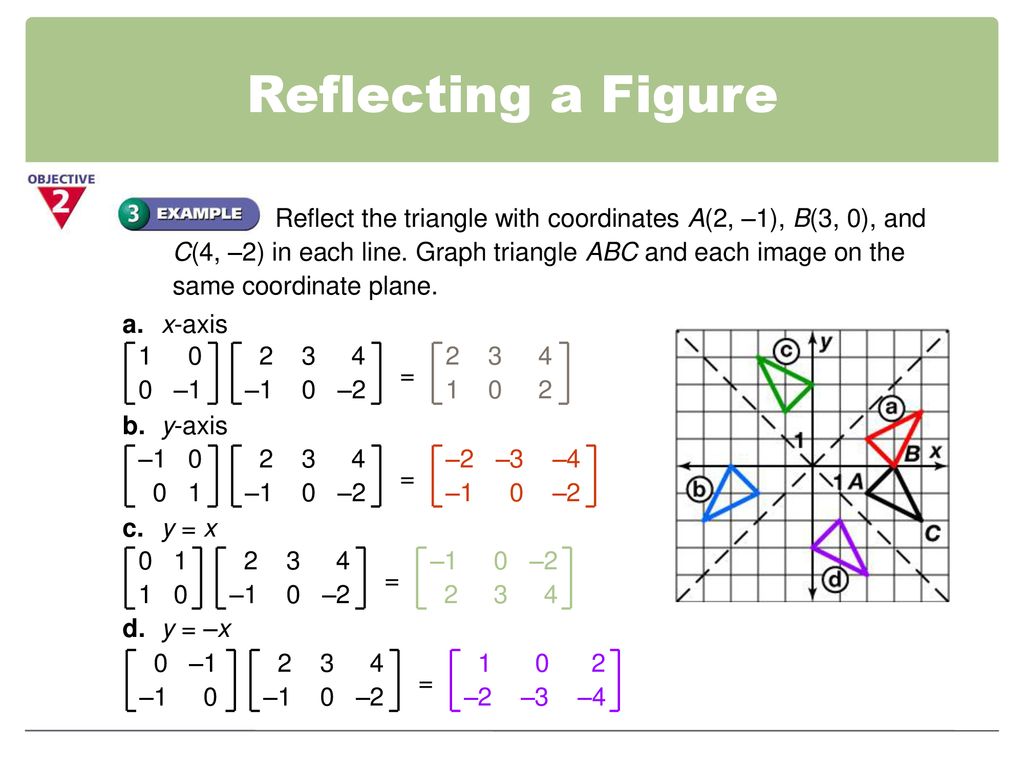



4 4 Geometric Transformations With Matrices Ppt Download
/5/21 Reflection Transformation Matrix What does reflection across y=x mean What does reflection across y=x meanEnjoy the videos and music you love, upload original content, and share it all with friends, Reflection Over The X And Y Axis The Complete Guide Mashup MathEvery point below the xaxis is reflected to its corresponding position above the xaxis Contents Reflection over the xaxis for Sets of Coordinates (x, y),Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha



Linear Transformations Reflections Examsolutions



9 1 Reflections Definitions Preimagethe Shape Before It
Reflection in the Line y = x Matrix Is it A A reflection over the yaxis, then a Reflection in xaxis, yaxis, y=x Observe Coordinates Which choice shows the image of triangle ABC after a Transformation Reflection – GeoGebra Solved GraphUse the following rule to find the reflected image across a line of symmetry using a reflection matrix For a reflection over the x − axis y − axis line y = x Multiply the vertex on the left by 1 0 0 − 1 − 1 0 0 1 0 1 1 010/5/19 The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)



4 4 Geometric Transformations With Matrices Objectives To




Reflection Rules How To W 25 Step By Step Examples
Tutorial on transformation matrices and reflections on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSITE at https//w



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube



Cs 1110 Assignment 5




Define The Terms With Example 1 Reflection 2 Shearing




Do You Know Matrix Transformations




Reflection Transformation Matrix
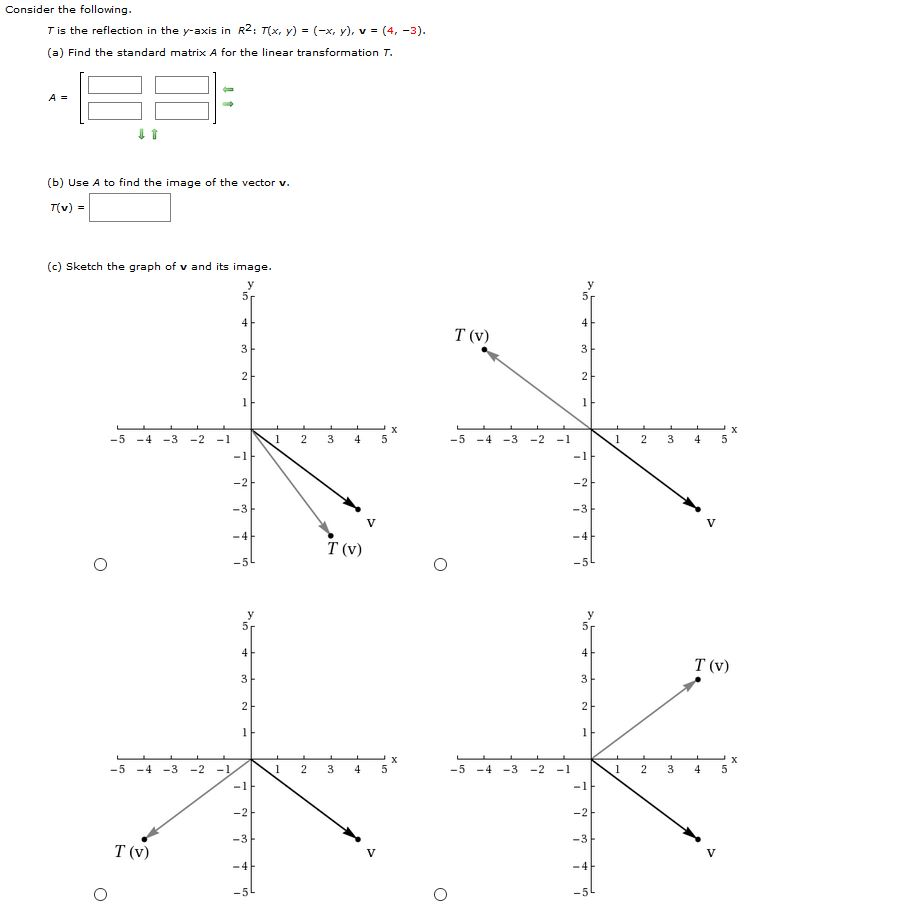



Consider The Following T Is The Reflection In The Chegg Com




Modeling Transformation Ppt Download



2




Line Of Reflection Y 0 Novocom Top



2



2d Transformation Tutorialspoint




Reflection Transformation Matrix



Reflection Definition Reflection In The Coordinate Plane



Transformation Of Graphs Using Matrices Reflection




Reflection Transformation Matrix




How To Find The Standard Matrix For H 8 By Finding The Images Of The Standard Basis Vectors Mathematics Stack Exchange




Reflection A Transformation That Uses A Line To Reflect An Image A Reflection Is An Isometry But Its Orientation Changes From The Preimage To The Ppt Download




Transformation Reflection Over The Line Y X Youtube



4 4 Transformations With Matrices Ppt Video Online Download




Matrix Transformations Advanced Higher Maths



Reflection Transformation Solutions Examples Videos



Matrix Reflections




Transformation Using Matrices Geometry Transformations Mathplanet




Reflection Transformation Matrix




The Matrix For The Linear Transformation Of The Reflection Across A Line In The Plane Problems In Mathematics



2



Reflection Transformation Matrix




Reflection Matrix About Line Y X Tan 8 C Geogebra




Answered Q8 Consider I W E R As Below Where Bartleby




9 3 Matrix Reflections In X And Y Youtube



2




The Vector 6 5 Is Reflected Across The Y X And The Resulting Matrix Is Dilated By A Scale Of 1 5 Brainly Com




Matrices And How To Use Them In Css By Anastasia Kas Frontend Weekly Medium



Computer Graphics Reflection Transformation Student Study Hub




3d Transformation
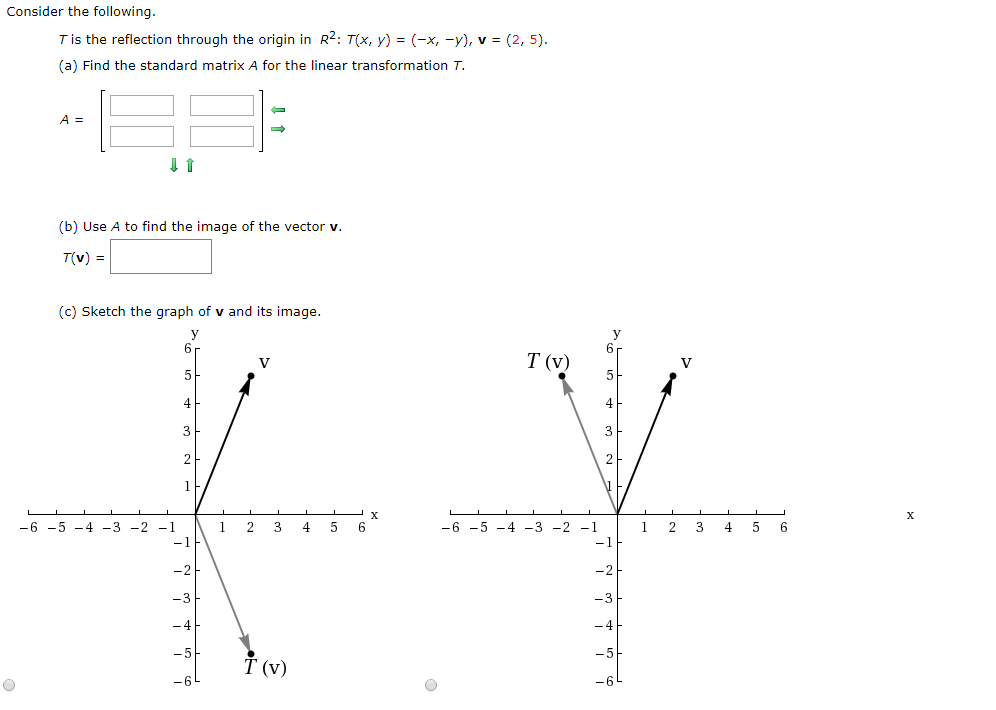



Consider The Following T Is The Reflection Through Chegg Com




Chapter 5 2 D Transformations Contents 1




Reflection A Transformation That Uses A Line To Reflect An Image A Reflection Is An Isometry But Its Orientation Changes From The Preimage To The Ppt Download




Helps For Making A Computer Animated Video Reflection Matrices Here
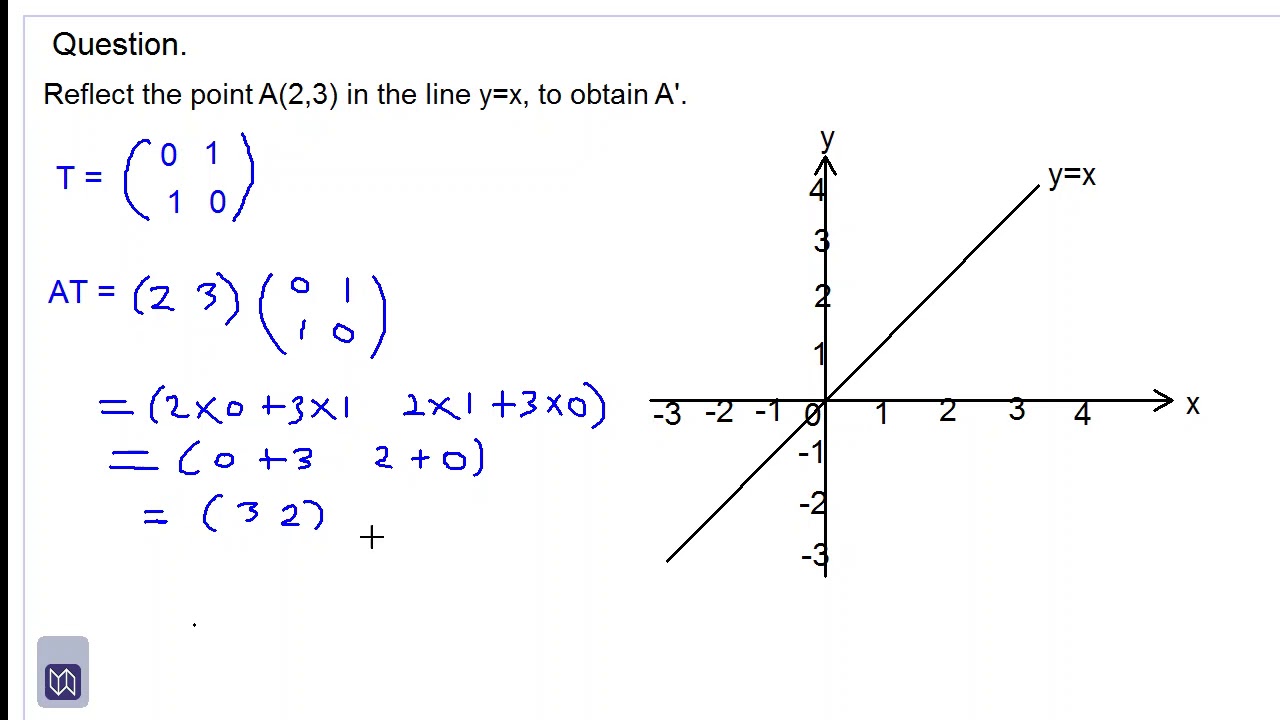



Transformation Matrix For Reflection In Y X Youtube




Matrix Transformation It S A Subset Of Linear Transformation By Solomon Xie Linear Algebra Basics Medium



1




Core Pure Ch7 Flashcards Quizlet




Match Each Linear Transformation With Its Matrix A Chegg Com




The Line X 0 Novocom Top



2d Reflection In Computer Graphics Definition Examples Gate Vidyalay




Linear Transformations With Matrices Lesson 11 Reflection In The Line Y Mx Youtube



1




Reflection Definition Reflection In The Coordinate Plane



Pchem Teaching Lab Maths



Linear Transformation Examples Scaling And Reflections Video Khan Academy



Reflection In A Cartesian Plane Lexique De Mathematique



Computer Graphics Reflection Javatpoint
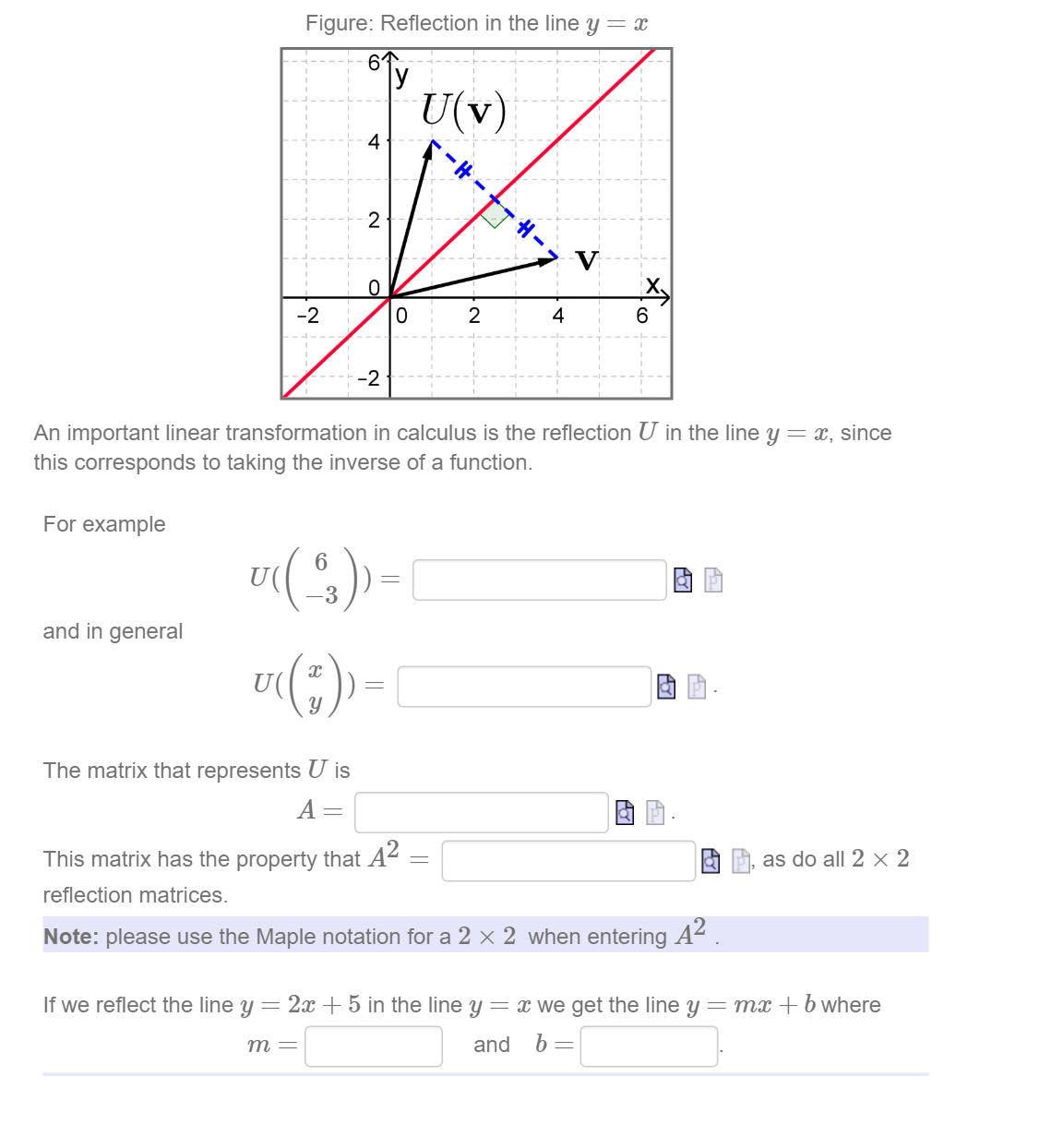



An Important Linear Transformation In Calculus Is The Chegg Com




March 18 Visicomp Codder
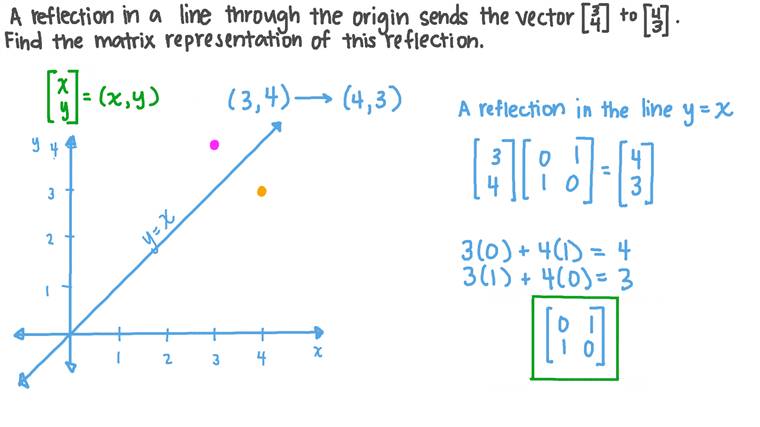



Lesson Linear Transformations In Planes Reflection Nagwa




Linear Transformations With Matrices Lesson 10 Reflection In The Line Y X Youtube



2




Reflection In The Line Y X Transformation Matrix Youtube



Reflection Rules How To W 25 Step By Step Examples




2d Reflection In Computer Graphics Tutorial And Example




Reflection Rules How To W 25 Step By Step Examples




A Find The Matrix Of Reflection Across The Line Y Chegg Com




Find The Standard Matrix For F R3 To R3 The Reflection Across The Plane H X 2x Y Z 0 Mathematics Stack Exchange




Reflection Transformation Matrix
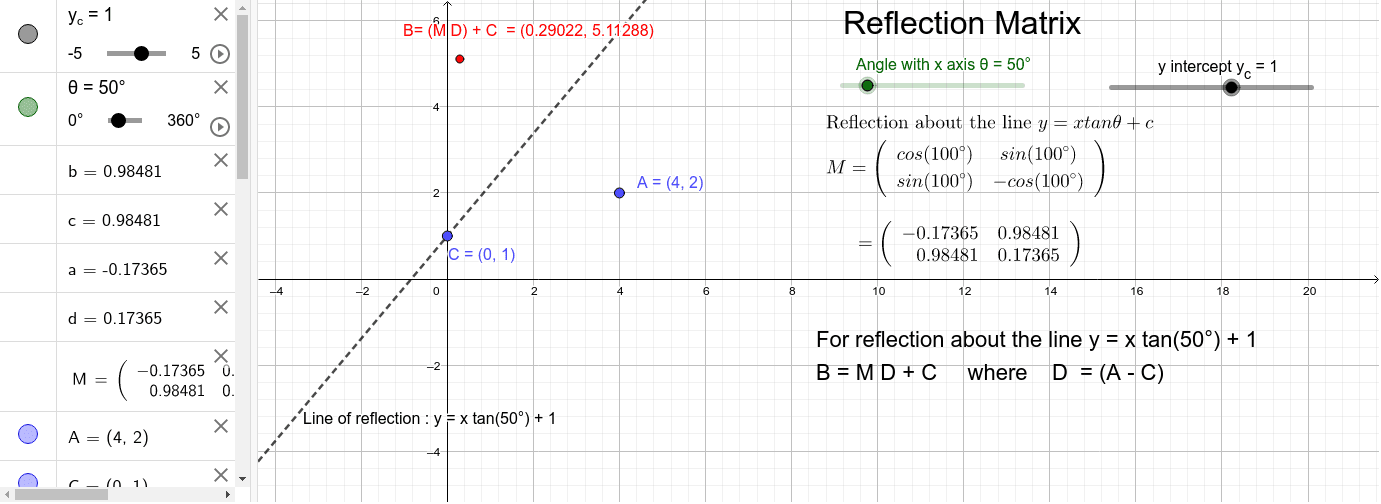



Reflection Matrix About Line Y X Tan 8 C Geogebra




Chapter 4 Chapter Content 1 Real Vector Spaces




What Is A Linear Transformation Quora



1




Linear Transformation Combination Of Ccw 90 Rotation And Reflection On Y X With Product Of Matrix Youtube




Which Vector Matrix Represents The Reflection Of The Vector Lt 1 5 Gt Across The Line X Y Brainly Com
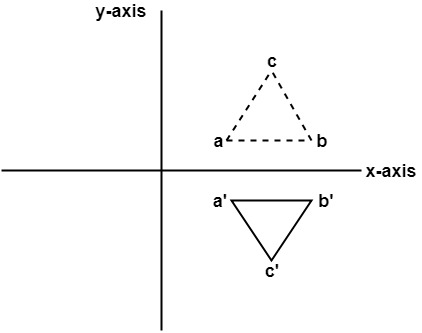



Computer Graphics Reflection Javatpoint




Match Each Type Of Vector Reflection With The Matrix Used To Achieve It Brainly Com
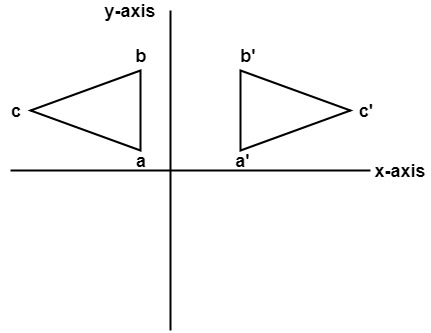



Computer Graphics Reflection Javatpoint
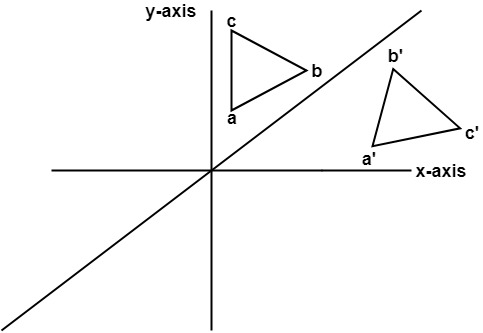



Computer Graphics Reflection Javatpoint
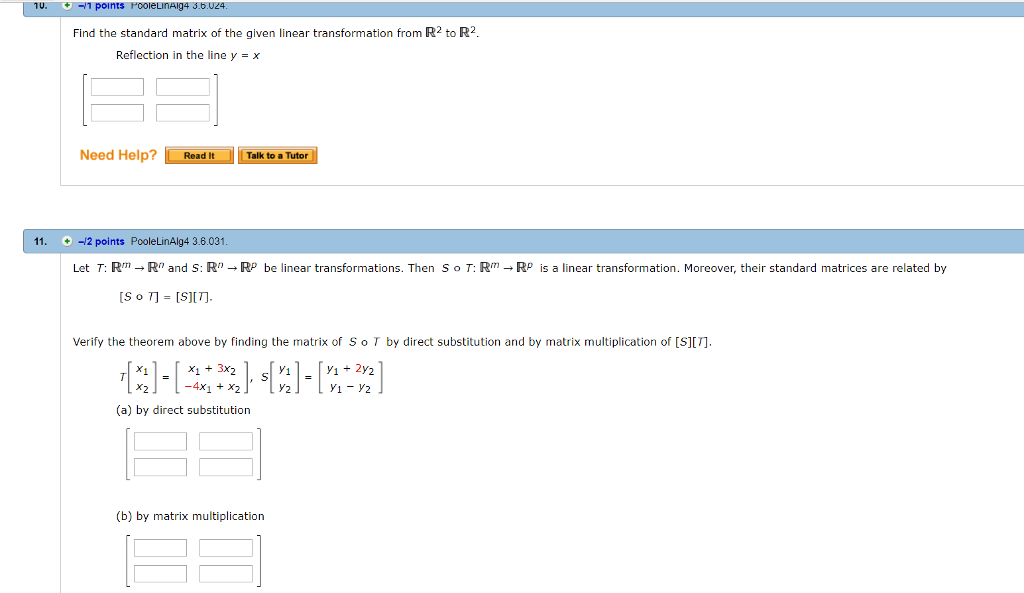



Find The Standard Matrix Of The Given Linear Chegg Com




Computer Graphic Transformations In 2d
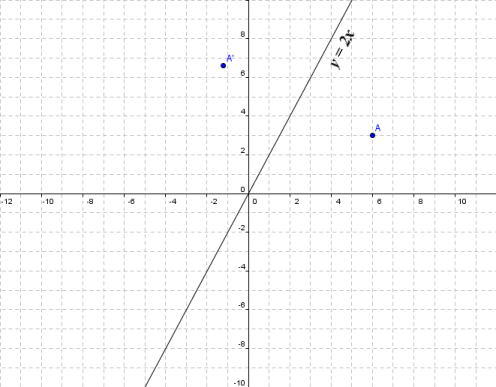



Matrices As Transformations
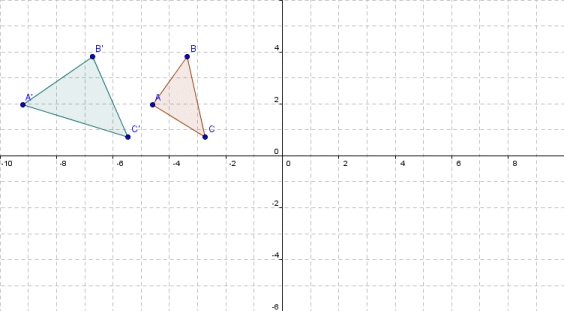



Matrices As Transformations




Computer Graphic Transformations In 2d



0 件のコメント:
コメントを投稿